¿Cuántos triángulos hay? Cómo resolver el rompecabezas
Este acertijo de cuantos triángulos hay no es nuevo, Popsugar lo desenterró hace un par de años.
No hay nada como un problema matemático enloquecedor, una ilusión óptica alucinante o un rompecabezas lógico retorcido para detener toda la productividad en SeCalcula. Somos personas curiosas por naturaleza, pero también compartimos colectivamente una obstinada insistencia en que tenemos razón, maldita sea , y por eso tendemos a dejar el trabajo por el camino cada vez que nos encontramos con un problema con varias soluciones aparentemente posibles.
Preguntamos cuantos triángulos hay
Dibujamos el triángulo de nuevo y les pedí a todos los miembros del equipo que dejaran rápidamente lo que estaban haciendo e intentaran resolver la pregunta simple: ¿Cuántos triángulos hay?
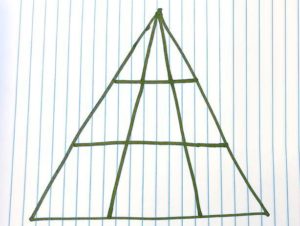
Te ahorraré la conversación completa, créeme, nadie quiere ver eso, pero las respuestas del equipo se extendieron por todos lados. Algunos editores vieron cuatro triángulos. Otros vieron 12. Algunos vieron 6, 16, 22. Incluso más vieron 18. Un hombre sabio contó los triángulos en las A en la pregunta en sí, mientras que otro parecía estar teniendo una crisis existencial: “Ninguna de estas líneas es realmente recta, sólo curvas, por lo que no se puede definir ninguna de ellas como un triángulo ”, dijo. “No hay triángulos en esta foto. La vida no tiene sentido «.
Podría haber escuchado a mis colegas explicar sus procesos cuestionables todo el día, pero en cambio, me comuniqué con varios expertos en geometría para ver si podíamos llegar a una respuesta de consenso. Resulta que prácticamente todos los matemáticos con los que contacté encontraron la misma solución, pero no todos la descubrieron de la misma manera.
Si aún no desea saber la respuesta, deje de leer e intente resolver el problema primero. Te veré aquí cuando hayas terminado.
¿Ya sabes cuántos triángulos hay?
A diferencia de algunos problemas matemáticos virales que son deliberadamente vagos y abiertos a la interpretación, este en realidad tiene una solución absoluta, sin lugar a dudas, y es 18. Escuchemos a algunos de los expertos en geometría por qué.
“Me acercaría a esto como se aborda cualquier problema matemático: reducirlo y encontrar la estructura”, dice Sylvester Eriksson-Bique, Ph.D., becario postdoctoral del departamento de matemáticas de la Universidad de California en Los Ángeles.
La única forma de formar triángulos en la figura que dibujé, dice Erikkson-Bisque, es si el vértice superior (esquina) es parte del triángulo. La base del triángulo tendrá que ser uno de los tres niveles siguientes. “Hay tres niveles, y en cada uno puede elegir una base entre seis formas diferentes. Esto da 18, o 3 veces 6 triángulos «.
Veamos nuevamente el triángulo maestro.
“Es conveniente generalizar al caso en el que hay n líneas que pasan por el vértice superior y p líneas horizontales”, dice Francis Bonahon, Ph.D., profesor de matemáticas en la Universidad del Sur de California.
En nuestro caso, n = 4 yp = 3. Cualquier triángulo que encontremos en el dibujo debe tener un vértice superior y otros dos en la misma línea horizontal, por lo que para cada línea horizontal, el número de triángulos con dos vértices en esa línea es igual al número de formas en que podemos elegir estos vértices, dice Bonahon, es decir, el número de formas en que podemos elegir dos puntos distintos de n , o » n elegir 2″.
¿Recuerdas las matemáticas de la escuela secundaria? Eso es n ( n -1) / 2. Y dado que hay p líneas horizontales, dice Bonahan, esto da pn ( n-1 ) / 2 triángulos posibles. En nuestro caso, eso es 3×4 (4-1) / 2 = 18.
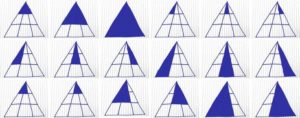
Solución visual a cuántos triángulos hay
Aquí hay un desglose útil de cómo encontrar cada triángulo posible:
