TOP Calculadoras:
Calcular el área de un trapecio
Utiliza esta calculadora para calcular fácilmente el área de un trapecio dados sus bases y altura.
Fórmula: A = ((b₁ + b₂) × h) ÷ 2
Área de un trapecio
El cálculo se basa esencialmente en el hecho de que el área de un trapecio se puede equiparar al de un rectángulo: (base 1 + base 2) / 2 es en realidad el ancho de un rectángulo con un área equivalente. Para utilizar nuestra calculadora del área de un trapecio, debes tomar tres medidas, todas en las mismas unidades (convierte según sea necesario).
El resultado siempre está en la unidad de longitud utilizada, pero al cuadrado. Por lo tanto, si mediste en pies, el resultado será en pies cuadrados. Si mediste en centímetros, el resultado será en centímetros cuadrados, y así sucesivamente para pulgadas cuadradas, yardas, millas, así como metros cuadrados, kilómetros…
Cálculo del área de un trapecio
Para realizar el cálculo, primero mide las dos bases. Luego, construye la altura utilizando un ángulo recto con una punta en cualquiera de las bases y utilizando esa base como uno de sus brazos. Mide la altura y realiza las conversiones métricas necesarias hasta que las tres longitudes estén en las mismas unidades.
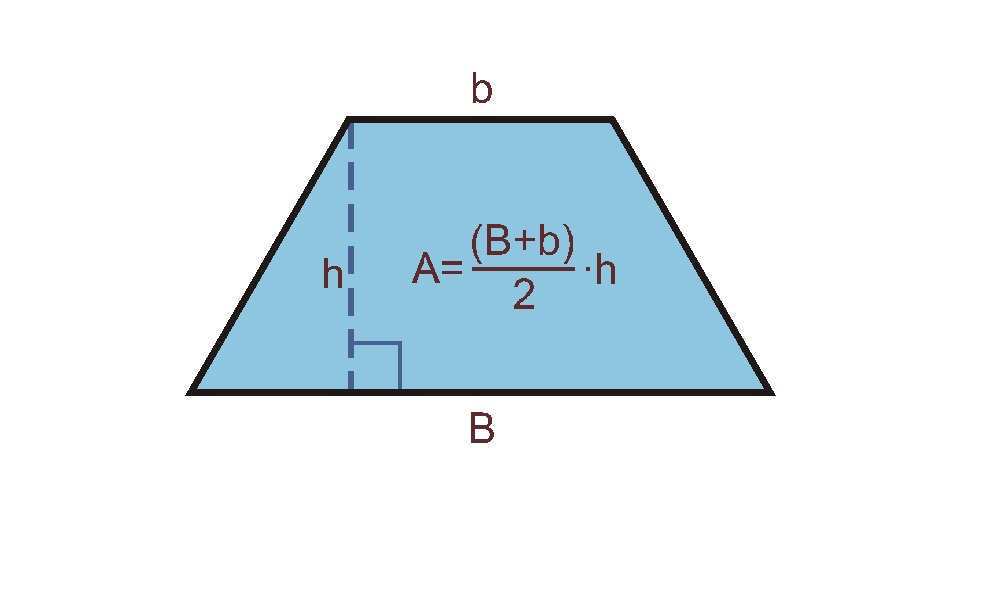
Luego aplica la fórmula anterior o utiliza nuestra calculadora en línea del área de un trapecio para ahorrar tiempo y tener una mayor probabilidad de que el resultado sea libre de errores (una mala entrada ciertamente dará como resultado una mala salida).
¿Qué es un trapecio?
Un trapezoide o trapecio es un cuadrilátero (una forma que tiene cuatro lados) que tiene al menos un par de lados opuestos paralelos entre sí. Observa que dijimos «al menos un par de lados» – si la forma tiene dos pares de lados paralelos, simplemente es un rectángulo. Y no te equivoques – todo rectángulo es un trapecio. Lo contrario, por supuesto, no es cierto.
Los dos lados, que son paralelos, suelen llamarse bases. Por lo general, dibujamos trapezoides de la manera que hicimos arriba, lo que podría sugerir por qué a menudo diferenciamos entre los dos diciendo base inferior y base superior. Los otros dos lados no paralelos se llaman catetos (similarmente a los dos lados de un triángulo rectángulo).
Queremos mencionar algunos casos especiales de trapecios aquí.
Rectángulo
Ya mencionamos esto al principio de esta sección – es un trapezoide que tiene dos pares de lados opuestos paralelos entre sí.
Trapecio isósceles
Un trapezoide cuyos catetos tienen la misma longitud (similarmente a cómo definimos triángulos isósceles).
Trapezoide recto
Un trapezoide cuyo cateto es perpendicular a las bases. En primer lugar, observa cómo requerimos aquí solo que uno de los catetos cumpla esta condición – el otro puede o no cumplirla. En segundo lugar, observa que si un cateto es perpendicular a una de las bases, entonces es automáticamente perpendicular a la otra también, ya que las dos son paralelas.
Con estos casos especiales en mente, un ojo atento podría observar que los rectángulos satisfacen las condiciones 2 y 3. De hecho, si alguien no sabía qué es un rectángulo, podríamos decir simplemente que es un trapecio isósceles que también es un trapezoide recto. Una definición bastante sofisticada en comparación con la habitual, pero seguro que nos hace sonar sofisticados, ¿no crees?
Hay dos segmentos de línea más que todos los trapezoides tienen.
La altura de un trapecio es la distancia entre las bases, es decir, la longitud de una línea que conecta las dos, que es perpendicular a ambas. De hecho, este valor es crucial cuando discutimos cómo calcular el área de un trapezoide y, por lo tanto, tiene su propia sección dedicada.
La mediana de un trapecio es la línea que conecta los puntos medios de los catetos. En otras palabras, con la imagen anterior en mente, es la línea que corta el trapezoide horizontalmente por la mitad. Siempre es paralela a las bases, y con la notación de la figura, tenemos mediana = (a + b) / 2. Si estás curioso sobre el nombre, asegúrate de revisar esta calculadora de mediana (nota: no se refiere a trapezoides).
Preguntas frecuentes sobre el área de un trapecio
Calculadoras relacionadas
Contenidos




